マクローリン展開の達人になろう！データサイエンス数学ストラテジスト（上級）公式問題集・問37を解説

2024年10月11日更新

本ページにはプロモーションが
含まれていることがあります

データサイエンス数学ストラテジスト（上級）の前半の問題は、大学レベルの数学の中でも特に計算量の多い、解くのにひとコツ必要なものが多いですね。その中から、解法自体はさほど難易度が高くはないものの、計算を工夫しないと正しく正解にたどりつけられない問37を解説します！

先に言いますと、解答は公式問題集で与えられたものとは異なりました。

私自身は実は、高度なアルゴリズムを操ることも図形（特に空間図形！）がとても好きとはいえません。その代わりに、微積分の計算（乱雑であればあるほどアドレナリンが湧いてきます）その他ゴリゴリ計算するタイプの問題が好きです。高校生の時は、クラスメイトと昼休みに因数分解の大会をやっていたほどです。本当に好き嫌いは性格そのものを反映しますね。

さて、今回は２パターンの計算法を示します。２通りでやって答えを検証したかったのと、相性のよいやり方は人ぞれぞれだからです。

自宅では、私は解法１で解いた→夫は解法２で解いた→私も解法２で解いて実感してみた、という流れで二人で認め合いました（笑）。

AI・データサイエンス、機械学習の
実践力を高めたい方へ

AI・データサイエンス・LLMアプリについて知りたい
AIエンジニア、データサイエンティストになりたい
DX化推進のための知識を身につけたい

AI人材コースを
無料体験してみませんか？

追加購入不要！これだけで学習できるカリキュラム

充実のサポート体制だから安心

2万円相当の基本講座をプレゼント！

▶AI人材コースを見る

自分のスキルに合わせたカリキュラムが生成できる！

理解度を記録して進捗管理できる！

テキストの重要箇所にハイライトを残せる！

1分で簡単！無料！

▶無料体験して特典を受け取る

問題37はどんな感じ？
解法1: ややスマートな置き換えをしようとした（果たして楽になったかどうかは…）
解法２：真面目に「普通」に計算
公式本の解答解説との違い

問題37はどんな感じ？

出典：データサイエンス数学ストラテジスト（上級）公式問題集　（日経BP）

ここでは、以下の式のマクローリン展開における　x⁴ の係数を求めたいわけです。

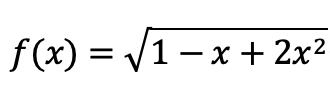
マクローリン展開とは簡単にいうと、テイラー展開のx＝０としたバージョンであり、の公式は以下の通りです。

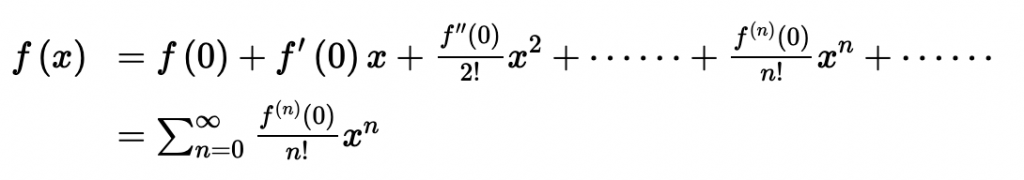
よって、求めたい、x⁴ の係数は　f⁽⁴⁾(0)/4! です。

f⁽⁴⁾(0)　はf(x) をxで４回微分した後にx=0とした値であり、分母の4! は「4の階乗」つまり、4!= 4・3・2・1 = 24 です。

解法1: ややスマートな置き換えをしようとした（果たして楽になったかどうかは…）

１回目の微分f'(x) までは真面目にやって、その結果をf(x) で表現し直したのがポイントです。この結果をさらに残りの計算に適用し、残り一連の計算を常に結果をf(x)で表そうとします。

ただ、今回の計算量では、この置き換えテクニックの有り難さを十分に感じることができていないかもしれません。とはいえ、知っておくとよいテクニックです。

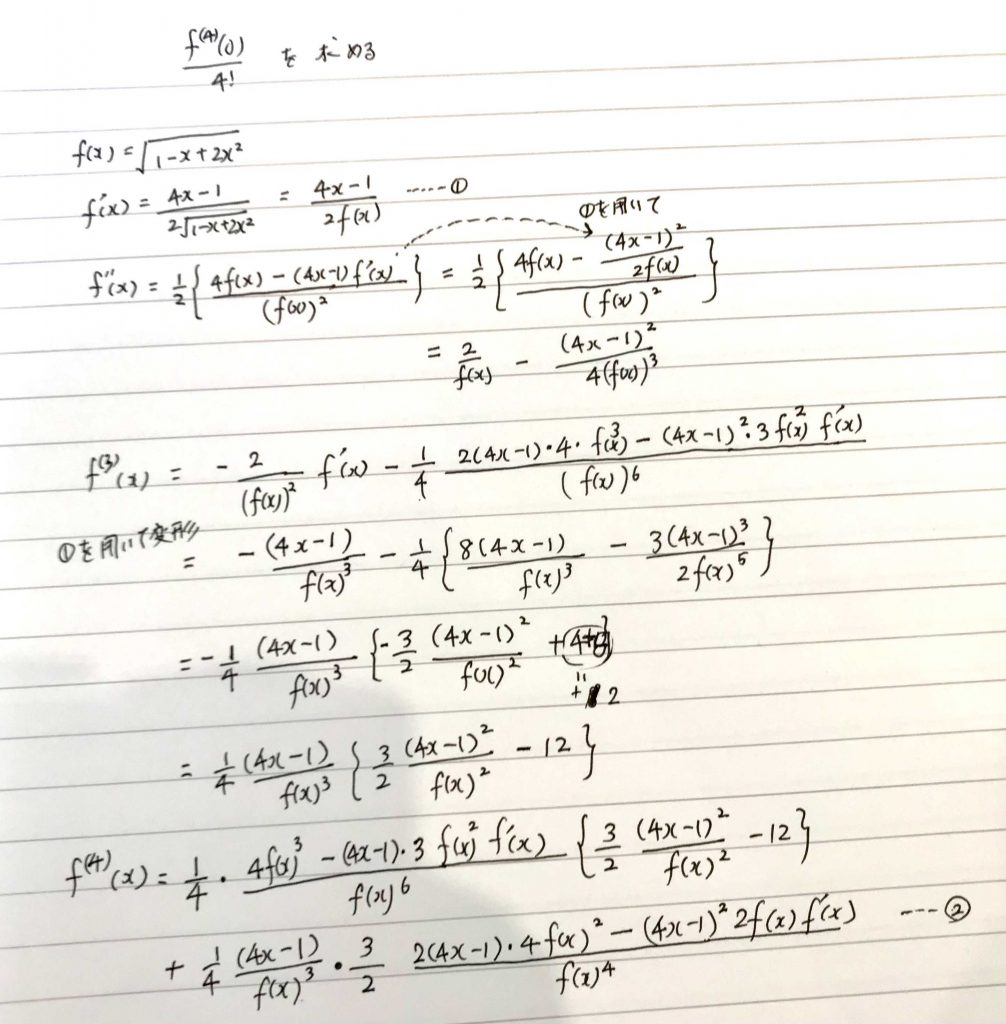
このプロセスの中で、f(x) をあたかも変数のように扱っているので、実際f(x)をその都度微分することを忘れないように注意しましょう。

f⁽⁴⁾(x)　まできたら、あとは0をあらゆる場所にあるxに代入し、一気に結果を簡略化します。ここでも計算間違い（特に符号）が発生しやすいので注意しましょう。

最終的に得られた答えは、x⁴ の係数は　f⁽⁴⁾(0)/4! = -21/128 です。

解法２：真面目に「普通」に計算

ここでは、f'(x) をf(x) で置き換えるようなことをせずに、普通に見た目の数式のままで微分を繰り返していきます。

６行目のあたりで中括弧の中を展開すると、案外スッキリしましたね。

解法１と解法２は同じ答え、f⁽⁴⁾(0)/4! = -21/128 が得られました。

公式本の解答解説との違い

公式本の解答と解説を拝見させていただきました。pg87の解説で下から３行目でしょうか … おそらくそちらで微分の後半において、誤植ではないかと思われる箇所があります。そのため、与えられた選択肢１〜５の中に今回の回答 -21/128 がありませんでした。